Hình học không gian là một chủ đề quan trọng trong giáo dục toán học. Điều này bao gồm việc xác định các đối tượng không gian bằng cách sử dụng các hình khối và các quy tắc liên quan đến chúng. Bài viết này sẽ giới thiệu về hình học không gian trong lớp 8 và cung cấp cho bạn các bài tập thực hành để giúp bạn hiểu rõ hơn về chủ đề này.
Tổng Quan Về Hình Học Không Gian Lớp 8
Khái niệm cơ bản về không gian và hình khối
- Không gian là một khái niệm trừu tượng đại diện cho một vùng trong không gian ba chiều.
- Hình khối là một hình học được tạo thành bởi các đường thẳng và mặt phẳng trong không gian ba chiều.
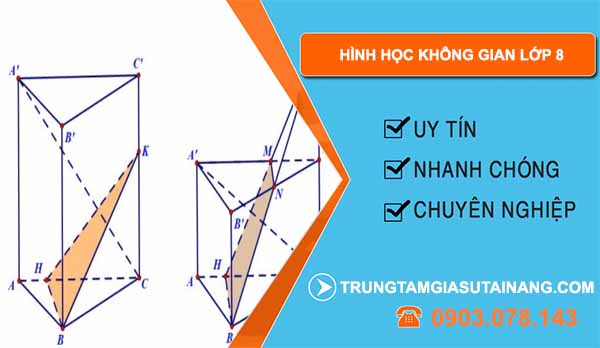
Các đối tượng không gian cơ bản
- Khối hộp
- Khối lăng trụ
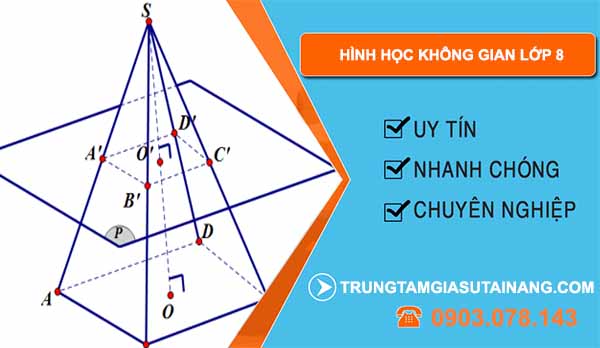
- Khối chóp
- Hình cầu
Các phép tính trong hình học không gian
- Thể tích của một hình khối
- Diện tích mặt phẳng của một hình khối
- Công thức Euler: F + V – E = 2
Bài Tập Thực Hành
Bài tập 1: Tính thể tích khối hộp
Cho khối hộp có chiều dài 3cm, chiều rộng 4cm và chiều cao 5cm. Hãy tính thể tích của khối hộp này.
Giải quyết:
Thể tích của khối hộp được tính bằng công thức:
V = l * w * h
Trong đó:
llà chiều dài của khối hộpwlà chiều rộng của khối hộphlà chiều cao của khối hộp
Thay vào giá trị đã cho, ta có:
V = 3cm * 4cm * 5cm = 60cm^3
Vậy thể tích của khối hộp là 60cm^3.
Bài tập 2: Tính diện tích mặt phẳng của khối lăng trụ
Cho khối lăng trụ có đáy là hình thoi có đường chéo dài 6cm và đường chéo nhỏ dài 4cm. Chiều cao của khối lăng trụ là 8cm. Hãy tính diện tích mặt phẳng của khối lăng trụ này.
Giải quyết:
Diện tích mặt phẳng của khối lăng trụ được tính bằng công thức:
S = 2 * S_{dn} + P_{day} * h
Trong đó:
S_{dn}là diện tích đáy của khối lăng trụP_{day}là chu vi đáy của khối lăng trụhlà chiều cao của khối lăng trụ
Đầu tiên, ta tính diện tích đáy của khối lăng trụ, do đáy là hình thoi nên ta có:
S_{dn} = \frac{d_{lon} * d_{nho}}{2}
Trong đó:
d_{lon}là đường chéo lớn của hình thoi đáyd_{nho}là đường chéo nhỏ của hình thoi đáy
Thay vào giá trị đã cho, ta có:
S_{dn} = \frac{6cm * 4cm}{2} = 12cm^2
Tiếp theo, ta tính chu vi đáy của khối lăng trụ, vì đáy của khối lăng trụ là hình thoi nên ta có:
P_{day} = 2 * (d_{lon} + d_{nho})
Thay vào giá trị đã cho, ta có:
P_{day} = 2 * (6cm + 4cm) = 20cm
Cuối cùng, ta tính diện tích mặt phẳng của khối lăng trụ bằng cách thay vào các giá trị đã tính vào công thức:
S = 2 * S_{dn} + P_{day} * h
Thay vào giá trị đã cho, ta có:
S = 2 * 12cm^2 + 20cm * 8cm = 176cm^2
Vậy diện tích mặt phẳng của khối lăng trụ là 176cm^2.
Những câu hỏi thường gặp
- Hình học không gian là gì?
- Hình học không gian là một chủ đề trong giáo dục toán học, liên quan đến việc định nghĩa các đối tượng không gian
- Những đối tượng không gian nào được sử dụng trong hình học không gian?
- Những đối tượng không gian thường được sử dụng trong hình học không gian bao gồm khối hộp, khối lăng trụ, khối chóp và hình cầu.
- Công thức tính thể tích khối hộp là gì?
- Công thức tính thể tích khối hộp là
V = a * b * c, trong đóa,b,clà các cạnh của khối hộp.
- Công thức tính diện tích mặt cầu là gì?
- Công thức tính diện tích mặt cầu là
S = 4 * pi * r^2, trong đórlà bán kính của hình cầu.
- Tại sao hình học không gian là một chủ đề quan trọng trong giáo dục toán học?
- Hình học không gian giúp cho học sinh hiểu được về không gian ba chiều và các đối tượng không gian trong cuộc sống thực. Nó cũng giúp học sinh phát triển khả năng tư duy không gian và giải quyết các bài toán thực tế liên quan đến không gian ba chiều.
Kết Luận
Hình học không gian là một chủ đề quan trọng trong giáo dục toán học. Các đối tượng không gian như khối hộp, khối lăng trụ, khối chóp và hình cầu được sử dụng để định nghĩa không gian ba chiều. Ngoài ra, các phép tính như thể tích, diện tích mặt phẳng và công thức Euler cũng được sử dụng để tính toán các đối tượng không gian này. Qua bài tập thực hành, bạn đã có thể áp dụng những kiến thức đã học để giải quyết các bài toán đơn giản về hình học không gian.

